Вероятность: основные понятия, структура, методы. - Скороход A.B.
Скачать (прямая ссылка):


1) для равномерной непрерывности х(6) на некотором
замкнутом множестве 01СГ0 необходимо и достаточно, чтобы
х(9) было равномерно непрерывно на в1ПЛ,
2) для ограниченности х(9) необходимо и достаточно, что-
бы х(9) было ограничено на Л,
3) если 0 — интервал прямой, то х(0) не имеет разрывов
второго рода, если х(9) на Л имеет для каждого е>0 конечное
число е-колебаний на Л, это означает, что для всякого е>0
можно указать такое к, что при п>&, каковы бы ни были
90<б1<. . .<9„ из Л,
Ы|>(л:(ег),л:(9г+1)), / = 0, 1, п— 1]<е.
Следующая теорема была доказана Дубом.
Теорема 2. Если в — сепарабельное метрическое про-
странство, X — компакт, то для всякой случайной функции су-
ществует сепарабельная модификация, т. е. можно указать не-
которое счетное плотное подмножество Лев, для которого су-
ществует Л-сепарабельная модификация.
Доказательство основывается на следующих соображениях.
Достаточно, чтобы соотношение (1) выполнялось для счетно-
го набора открытых множеств £/йсгв (образующих базу от-
крытых множеств в в) и счетного набора замкнутых множеств
FhczX (дополнения которых образуют базу открытых множеств
в X).
Если для каждой пары k, т построим такое множество
Ah,m, что
Р/ П {м:х*(9, to)6Fm}\ П (со:х*(9, <o)eF„}=*(), (2)
где x* — некоторая модификация х, то, беря Л= U А&,п,
к,т
S=\J ( П {w:x*(9, co)6Fm}\ П {<o:x*(Q, co)eFm}\, (3)
убеждаемся, что P(S)=0.
Задача сводится к построению множеств Аи,т, чтобы выпол-
нялось (2), и самой модификации х*.
Лемма. Для всякого Uk Fm можно построить такое Ak,m>
что для всех 9614
Р{хф, ш)б/7т, ееЛ*,т, х(е)ё/гт} = 0.
Доказательство. Если 9i, 92,..., 8П уже выбраны, то
выберем Qn+i^Uk так, чтобы
P{x(Qi, a)eFm, / = 1,2,...,«, х(9„+], ®)6Fm}>
>~sup P{x(Q{, (o)£Fm, i = 17«, x% <x>jeFm}.
Ряд из вероятностей слева сходится, так как это ряд из веро-
ятностей несовместимых событий. Значит, его общий член стре-
мится к нулю и, полагая Ak,m={6i, 82,...}, получим доказа-
тельство леммы.
Построим теперь нужную модификацию. Пусть Ak=\jAk,m.
т
Обозначим через /)*(м) замыкание множества {x(Q, со), 9бЛ4} (оно
зависит от со). Положим £)9(со) = fl Dft(co). Это непустое мно-
жество, так как X компакт. Пусть х*(9, со) = х(9, со), если
х (9, со)б£>е(со), х* (9, со)б/)е (со) выбрано произвольно, если
■£(9, со)б£)е. Это и будет нужная модификация.
1.2. Непрерывные случайные процессы. Рассмотрим случай-
ный процесс x(t, со), определенный на некотором множестве
Тс/? со значениями в полном метрическом сепарабельном
пространстве X. Если он имеет непрерывную модификацию, бу-
дем называть его просто непрерывным. Для доказательства не-
прерывности процесса на Т достаточно доказать, что он рав-
номерно непрерывен на некотором счетном плотном подмно-
жестве Т0сТ, т. е.
P{lim sup r{x(tu со), x(t2, со)) = 0}=1. (4)
В этом случае существует
lim x(t', (м) = х*((, со)
с вероятностью 1 для всех /бГ, и x*(t, со) и будет непрерывной
модификацией.
Теорема 3 (Колмогоров). Пусть 7= [0,1] и существуют
такие а>0, ß>0, А>0, что
mrt(x(t, со), x(s, ti>))s^k\t—s|1+a. (5)
Тогда процесс x(t, со) непрерывен.
Доказательство. Пусть Т0 — множество двоично ра-
циональных чисел. Покажем, что x(t, со) равномерно непреры-
вен на Tq. Положим у
Л„ = sup^r [x(Jp, со), х(^-, со)).
Тогда при 0<а< 1
Р{Ля>а"}<2 PH^(i". &))>а"}<
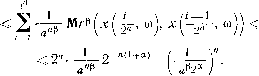
а
Выбирая теперь а>2 р, получим, что ^Р{т)л>а"}< оэ, а зна-
чит, на основании теоремы Бореля—Кантелли для достаточно
больших п г|„<а'г. Остается заметить, что при 0 = ^йг> 1^2—
<-^т. *2=^,/1>т будет г (л (*ь со), д:(*2, <о))<лт+1+ - ..4-Ля-
со
Поэтому для любых *ь *26Г0 г(-*:(г'ь т)> *(*2> со))<2 2 Чй, где
.от таково, что 1/2т>|^2 —^1 |>1/2т+1. Отсюда вытекает
утверждение теоремы. □
1.3. Процессы без разрывов второго рода. Рассмотрим опять
случайный процесс на [0, 1] с фазовым пространством X, яв-
ляющимся сепарабельным полным метрическим пространст-
вом. Процесс x{t,&) не имеет разрывов второго рода, если на
некотором плотном множестве Го для почти всех со существу-
ют пределы
lim x(t', со), lim x(t', со),
t'it.t'QT,, t'it0,t'QT0
которые будут в дальнейшем обозначаться x(t—, со) и
x(t-\-, со). В этом случае, полагая х* (t, со) =x(t—, со), если в
точке t процесс стохастически непрерывен слева, х* (t, со) =
= x(t-\-, со), если он стохастически непрерывен справа в точке
t (но не стохастически непрерывен слева), х*(t, со) —x(t, со),
если нет стохастической непрерывности ни слева ни справа,
получим модификацию процесса x(t, со) без разрывов второго
рода. Для ее существования необходимо и достаточно, чтобы
для всякого е>0 процесс x(t,(o) имел с вероятностью 1 ко-
нечное число е-колебаний на 7V


